The next phase for Genicap’s Ecosystem: 1. Analysis

In the next phase the applicability will be exploding since now we have also the ability to include the analysis step, to turn shapes and signals into the parameters of the Formula, by scanning shapes or analysing time series from various in a most effective way. The original Gielis Formula was very effective in analysing shapes without a priori knowledge encoded into the computer program, but this lacked in efficiency and computational time. Also this is now amended via another important development, in collaboration with the University of Antwerp.
The original work by University of Antwerp has been extended to a firm collaboration, and, additionally, into a new patent by Genicap. It allows for an extremely efficient encoding of time series or data in terms of damped exponentials, very closely allied to the Generalized Gielis Formula. It can be used in a wide range of applications, more efficiently than comparable algorithms or methods. Examples of applications include motor fault diagnosis, power system transient detection in grids, magnetic resonance / infrared spectroscopy, vibration and seismic data analysis, music signal processing, corrosion rate / crack initiation, odour recognition with electronic nose, typed keystroke recognition, liquid (explosive) identification, direction of arrival of signals and many other applications. It can be used in an extremely wide variety of settings and industrial applications, even more so in combination with Gielis Formula.
A key component is that sampling can be very sparse, below Nyquist boundaries. Normally this would create aliasing, but not so with the new methods, which are also computationally efficient and fast. So, less data are needed for more accurate modelling and data understanding. One example is shown in Figure 1, whereby

Figure 1

The mathematical theory behind it is closely related to the Gielis Formula, and like the Formula, it provides a solution to a 200 year-old problem, studied for the first time in Paris around 1800-1820. It has the potential to solve the curse of multidimensionality, so immediately can be used for existing ideas in the Genicap environment, e.g. the patent family around databases. In particular, the results can be interpreted physically, i.e. as solution of differential equations, in terms of polynomials or special functions, in contrast to the current results by using Fourier or wavelet transforms. In Figure 2 it is shown

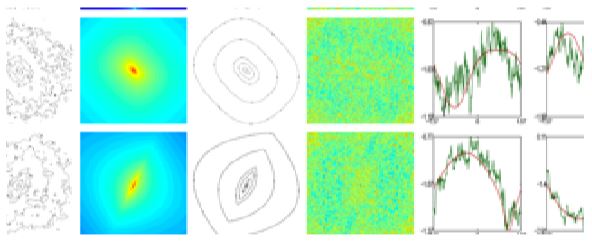
Figure 2: colour intensity maps display clear superformula fingerprint.

In particular, it can be used for efficient determination of computationally intensive data collections and processing. In the next 6 months processing trials are planned and excecuted, and it is not unreasonable to expect that computational effort and necessary memory can be reduced by 50% or more.

Figure 3: colour intensity maps display clear superformula fingerprint.